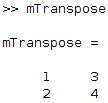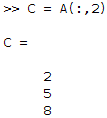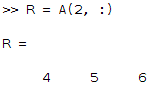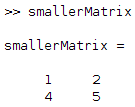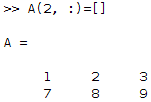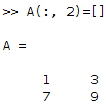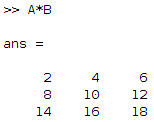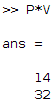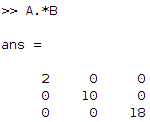This article explains the key points of manipulating MATLAB matrices when starting. Specifically, you’ll learn to:

  • Create a matrix
    • Define a matrix
    • Get the dimensions of a matrix
  • Inverse, transpose, and extract elements from a matrix and create the identity matrix
    • Transpose a matrix
    • Inverse of a matrix
    • Define the identity matrix
    • Extract data from a matrix
  • Multiply matrices
    • Square matrix
    • Non-square matrix
    • Multiply matrices element by element

Create a Matrix in MATLAB

Define a Matrix

Let’s start by defining matrices. The first thing to know is that you can separate rows by semi-colons (;) and that you define rows by just placing elements next to one another. Then, use square brackets to mark the beginning and the end of your matrix. For example, let’s say you have the following matrix:

\(m=\begin{pmatrix}1 & 2\\3 & 4\end{pmatrix}\)

You can define it as the following in Matlab:

m = [1 2 ; 3 4];

Dimensions of a Matrix

You can find the dimension of a matrix by using the MATLAB command size. You can determine the number of rows and the number of columns of your matrix with the following:

numberOfRows = size(m, 1); 
numberOfColumns = size(m, 2);

in MATLAB, we get:

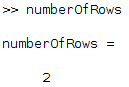
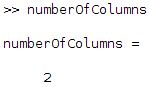
nomber of rows in a matrix using sizeNumber of columns in a matrix using the size MATLAB command

MATLAB Matrix: Inverse, Transpose, and Identity Matrix and Extracting Elements

The Transpose MATLAB Function

  • Transpose matrix: you can use the transpose function in MATLAB by adding a single quotation mark at the end of your matrix: 
    m = [1 2 ; 3 4];
mTranspose = m';

    In MATLAB, we get
    transpose matlab command example on matrix m

  • Transpose vector: this can be used to transform a row vector into a column vector as follows: 
     columnVector = rowVector'; % transform a row vector into a column vector

    In this article, we focus on matrices in MATLAB, so we won’t get into much detail about vectors. If you want to learn more about vectors, see: MATLAB Vector Tutorial: Create, Add, Concatenate and Extract

The Inverse MATLAB Function

You can inverse a matrix by using the inv MATLAB command:

m = [1 2 ; 3 4];
mInverse = inv(m);

By definition, if we multiply those 2 matrices, we should get the identity matrix:
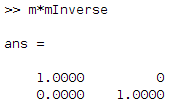
example of inverse matrix using inv

The Identity Matrix In MATLAB

You can define the identity matrix with the eye MATLAB function. For example, if you want to have a matrix function identity of three columns and three rows (\(I_3\)), you can write:

 identityMatrix = eye(3); % identity square matrix 3x3

Extract Data from a Matrix

Sometimes, you will have to extract a row or a column from a matrix. Let’s say you have the following matrix:

\(A = \begin{pmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{pmatrix}\)

Defined in MATLAB as the following:

A = [1 2 3 ; 4 5 6 ; 7 8 9];
  • Extract a column from a matrix: For example, if you have a matrix that has three columns and you want the second column, you can do the following: 
    C = A(:,2) % select all rows (:) and only the second column (2)

    In MATLAB, we get
    extract the second column of a matrix

  • Extract a row from a matrix: if you want to extract the second row, you can do the following: 
    R = A(2, :) % select only the second row (2) and all columns (:)

    In MATLAB, we get
    extract the second row of a matrix

  • Extract a smaller matrix: if you want a square matrix of two rows and two columns extracted from A, you can do the following: 
     smallerMatrix = A(1:2, 1:2); % extract columns and rows 1 to 2

    You will then have the first two rows and the first two columns of your previous matrix:extract a matrix from a bigger one

  • Remove a column or a row from a matrix: you can also remove data from a matrix such as a column or a row: 
    A(2, :)=[]; % remove the second row
A(:, 2)=[]; % remove the second column

    Note that the order matters since we are removing the second row of A:
    remove a row from a matrix in matlab
    Then, we remove the second column of that new matrix (which is not A as we defined it):
    remove a column from a matrix in matlab

Matrix Multiplication In MATLAB

Multipliying Matrices in MATLAB: Square Matrix

  • Code for matrix multiplication: you can multiply matrices in MATLAB by using the following: 
     A*B % classic matrix multiplication in MATLAB
  • Example of matrix multiplication: if we have these matrices:

    \(A = \begin{pmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{pmatrix}~~~~~~And~~~~~~B = \begin{pmatrix}2 & 0 & 0\\0 & 2 & 0\\0 & 0 & 2\end{pmatrix}\)

    Let’s multiply them in MATLAB:

    A = [1 2 3 ; 4 5 6 ; 7 8 9];
B = [2 0 0 ; 0 2 0 ; 0 0 2]; % = 2*identityMatrix
A*B

    Then, in MATLAB, we get
    multiply matrix A and B in matlab

  • Interpretation: according to MATLAB, AB=2A. This makes sense, since

    \(B = \begin{pmatrix}2 & 0 & 0\\0 & 2 & 0\\0 & 0 & 2\end{pmatrix} = 2I_3 \implies A\times B = A\times 2I_3=2\times A\)

Multiplying Matrices With Vectors and Non-Square Matrices

  • Reminder: you can also multiply non-square matrices with each other (e.g. a matrix with a vector). If you multiply a matrix P of dimensions (m x n) with a matrix V of dimensions (n x p) you’ll get a matrix of dimension (m x p).
  • Example of non-square matrix multiplication: let’s say you have the following matrices:

    \(P = \begin{pmatrix}1 & 2 & 3\\4 & 5 & 6\end{pmatrix}~~~~~~And~~~~~~V = \begin{pmatrix}1\\2\\3\end{pmatrix}\)

    Then, P*V will be

    \(P\times V = \begin{pmatrix}1 & 2 & 3\\4 & 5 & 6\end{pmatrix}\begin{pmatrix}1\\2\\3\end{pmatrix}=\begin{pmatrix}1\times 1 +2\times 2 + 3\times 3\\4\times 1+5\times 2 + 6\times 3\end{pmatrix}=\begin{pmatrix}14\\32\end{pmatrix}\)

  • Non-square matrix multiplication in MATLAB: let’s try it: 
    P = [1 2 3 ; 4 5 6]; % P is a (2x3) matrix 
V = [1 ; 2 ; 3]; % V is a (3x1) non square matrix (or vector)
P*V

    We get
    matlab matrix mulitplication example for non square matrix
    Since P is a (2×3) matrix and V is a (3×1) matrix, P*V is a (2×1) matrix.

Multiplying Matrices by Elements

  • Reminder: you can also multiply matrices element by element. Let’s see how it works with the example of A and B:

    \(A = \begin{pmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{pmatrix}~~~~~~And~~~~~~B = \begin{pmatrix}2 & 0 & 0\\0 & 2 & 0\\0 & 0 & 2\end{pmatrix}\)

    Every element of the matrix A would be multiplied by the corresponding element in matrix B. In our example, we would have:

    \(\begin{pmatrix}1 \times 2 & 2\times 0 & 3\times 0\\4\times 0 & 5\times 2 & 6\times 0\\7\times 0 & 8\times 0 & 9\times 2\end{pmatrix}=\begin{pmatrix}2 & 0 & 0\\ 0 & 10 & 0\\0 & 0 & 18\end{pmatrix}\)

    which means that the matrices that are multiplied have to be of the same size.

  • MATLAB matrix multiplication element by element: the element-wise matrix multiplication of A by B would be: 
    A = [1 2 3 ; 4 5 6 ; 7 8 9];
B = [2 0 0 ; 0 2 0 ; 0 0 2]; % = 2*identityMatrix
A.*B

    We get
    MATLAB matrix multiplication element by element

Key takeaways:

    1. Create a matrix using the following: 
      m = [1 2 ; 3 4]; % separate columns by a space and rows by a semi-colon
    2. Get the dimensions of a matrix using: 
      size(m, 1) % number of rows
size(m, 2) % number of columns
    3. MATLAB matrix: transpose, inverse and identity matrix: 
      m = [1 2 ; 3 4];
mTranspose = m'; % transpose matrix
mInverse = inv(m); % inverse matrix
identityMatrix = eye(n); % identity square matrix (nxn)
    4. Extract data from a matrix: 
      A = [1 2 3 ; 4 5 6 ; 7 8 9];
C = A(:,2) % select all rows (:) and only the second column (2)
R = A(2, :) % select only the second row (2) and all columns (:)
smallerMatrix = A(1:2, 1:2);
A(2, :)=[]; % remove the second row
A(:, 2)=[]; % remove the second column
    5. Multiply a matrix: using A*B or A.*B for element-wise multiplication: 
      A*B % classic matrix multiplication
A.*B % element by element matrix multiplication

Jacob Sapir
Jacob Sapir